A)
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use NINT on a calculator to find the numerical integral of the function over the specified interval. - Round to three decimal places.
A)
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use graphs and tables to find the limit and identify any vertical asymptotes. -
A) 9 ; no vertical asymptotes
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Compute the average of the RRAM and LRAM approximations to estimate the area between the graph of the function and the x-axis over the given interval using the indicated number of subintervals. (The function is non-negative on the given interval) . - subintervals
A)
B) 115
C) 230
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function at the specified point. - at
A) 0
B) 5
C) 10
D) 9
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The position of an object at time is given by . Find the instantaneous velocity at the indicated value of . t at
A) 5
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit. -Let and . Find .
A) 5
B) 2
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the indicated limit. -
A)
B) 0
C)
D) 1
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the definite integral by computing an area. -
A) 175
B) 35
C)
D)
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A toy rocket is launched straight up from level ground. Its velocity function is , where is the number of seconds after launch. At what time does the rocket reach its maximum height?
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Match the function with the correct table values.
-
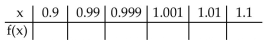
A)
B)
C)
E) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function at the specified point. - at
A)
B)
C) 8
D) 2
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem.
-Estimate the "RRAM" area under the graph of the function above the -axis and under the graph of the function from to . Use 5 subintervals.
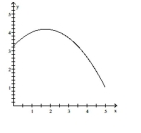
A) 15.5
B) 18.75
C) 17.5
D) 14.5
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function at the specified point. - at
A) 8
B) 3
C) 7
D) 6
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Match the function with the correct table values.
-
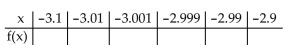
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit of the function by using direct substitution. -
A) 0
B) 1
C)
D)
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the derivative of the function using the definition of derivative. -
A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the equation of the tangent line to the curve when x has the given value. -
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use NDER on a calculator to find the numerical derivative of the function at the specified point. - at
A) 3
B)
C)
D) 33
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the limit of the function algebraically. -
A) Does not exist
B)
C) 0
D) 5
F) None of the above
Correct Answer

verified
Correct Answer
verified
Showing 101 - 120 of 167
Related Exams